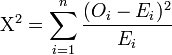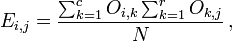Today, when running a mapreduce job on 4 Amazon m1.xlarge nodes. Got the fallowing error.
java.io.IOException: Cannot run program "bash": java.io.IOException: error=12, Cannot allocate memory
java.lang.Throwable: Child Error
at org.apache.hadoop.mapred.TaskRunner.run(TaskRunner.java:532)
As amazon instance doesn't provide any swap space which means all the process are stay fully in memory all the time. It's very easy to cause memory problems. TO solve the above errors. Simply add swap space in your amazon instance.
Another course could be overload nodes, it's very important to have a proper task numbers, overloaded nodes may lead to memory problems too.
Tuesday 27 March 2012
A Glance at the Hadoop Failure Model
A Glance at the Hadoop Failure Model
Hadoop is designed to be a fault tolerant system. Jobs should be resilient to nodes going down and other random failures. Hadoop isn’t perfect however, as I still see jobs failing due to random causes every now and again. I decided to investigate the significance of the different factors that play into a job failing.A Hadoop job fails if the same task fails some predetermined amount of times (by default, four). This is set through the properties “mapred.map.max.attempts” and “mapred.reduce.max.attempts”. For a job to fail randomly, an individual task will need to fail randomly this predetermined amount of times. A task can fail randomly for a variety of reasons – a few of the ones we’ve seen are disks getting full, a variety of bugs in Hadoop, and hardware failures.
The formula for the probability of a job failing randomly can be derived as follows:
Pr[individual task failing maximum #times] = Pr[task failing] ^ (max task failures)
Pr[task succeeding] = 1 - Pr[individual task failing maximum #times]
Pr[job succeeding] = Pr[task succeeding] ^ (num tasks)
Pr[job failing] = 1 - Pr[job succeeding]Pr[job failing] = 1 - (1-Pr[task failing] ^ (max task failures))^(num tasks)
The maximum amount of task failures is set through the property “mapred.max.tracker.failures” and defaults to 4.
Let’s take a significant workload of 100,000 map tasks and see what the numbers look like:

As the probability of a task failing goes above 1%, the probability of the job failing rapidly increases. It is very important to keep the cluster stable and keep the failure rate relatively small, as these numbers show Hadoop’s failure model only goes so far. We can also see the importance of the “max task failures” parameter, as values under 4 cause the probability of job failures to rise to significant values even with a 0.5% probability of task failure.
Reducers run for a much longer period of time than mappers, which means a reducer has more time for a random event to cause it to fail. We can therefore say that the probability of a reducer failing is much higher than a mapper failing. This is balanced out by the fact that there are a much smaller amount of reducers. Let’s look at some numbers more representative of a job failing due to reducers failing:

The probabilities of a reducer failing need to go up to 10% to have a significant chance of failure.
Bad Nodes
One more variable to consider in the model is bad nodes. Oftentimes nodes go bad and every task run on them fails, whether because of a disk going bad, the disk filling up, or other causes. With a bad node, you typically see a handful of mappers and reducers fail before the node gets blacklisted and no more tasks are assigned to it. In order to simplify our analysis, let’s assume that each bad node causes a fixed number of tasks to fail. Additionally, let’s assume a task can only be affected by a bad node once, which is reasonable because nodes are blacklisted fairly quickly. Let’s call the tasks which fail once due to a bad node “b-tasks” and the other tasks “n-tasks”. A “b-task” starts with one failure, so it needs to fail randomly “max task failures – 1″ times to cause the job to fail. On our cluster, we typically see a bad node cause three tasks to automatically fail, so using that number the modified formula ends up looking like:
#b-tasks = #bad nodes * 3
Pr[all b-tasks succeeding] = (1-Pr[task failing] ^ (max task failures - 1))^(#b-tasks)
Pr[all n-tasks succeeding] = (1-Pr[task failing] ^ (max task failures))^(num tasks - #b-tasks)
Pr[job succeeding] = Pr[all b-tasks succeeding] * Pr[all n-tasks succeeding]
Pr[job succeeding] = (1-Pr[task failing] ^ (max task failures -
1))^(#b-tasks) * (1-Pr[task failing] ^ (max task failures))^(num tasks -
#b-tasks)
Pr[job failing] = 1 - Pr[job succeeding]Pr[job failing] = 1 - (1-Pr[task failing] ^ (max task failures - 1))^(#b-tasks) * (1-Pr[task failing] ^ (max task failures))^(num tasks - #b-tasks)
Since there are so many mappers, the results of the formula won’t change for a handful of bad nodes. Given that the number of reducers is relatively small though, the numbers do change somewhat:

Happily the numbers aren’t too drastic – five bad nodes causes the failure rate to increase by 1.5x to 2x.
In the end, Hadoop is fairly fault tolerant as long as the probability of a task failing is kept relatively low. Based on the numbers we’ve looked at, 4 is a good value to use for “max task failures”, and you should start worrying about cluster stability when the task failure rate approaches 1%. You could always increase the “max task failures” properties to increase robustness, but if you are having that many failures you will be suffering performance penalties and would be better off making your cluster more stable.
Saturday 10 March 2012
Rails study notes 1
Rails as as MVC fraework
model view controller
controller(models.rb) rails routing
1. Routes map incoming url's to controller actions
2. controller actions set instance vairables, visible to views
3. controller action enventually renders a view
Convention over configuration: if naming follows certain conventions, no need for config files
Don't repear yourself: mechanisms to exract common functionality
Database:
Rails feature:
Testing: develpment and production and test enviroments each have own DB
Mirgration: scripts to descripe the change
up version and down version of migration methods, that makes everything reversible
Apply migration to development:
rake db:migrate
Add a new model
rails generate migration
Raisl generate sql statement at runtime, based on ruby code
Subclassing from ActiveRecord::Base
connects a model to a database
Reading things in the database
Movie.where("rating = 'PG')
Add a action
1. create route in config/routes.rb
2. Add the action in the apporcatia place
3. add the view coresspondinly
Debug
Printing to termial
log file
when debugging, the error information can be very useful, the information could tell us where th error is in the ruby.
Don't use puts or printf to print error message, as they may just been print out on the terminal, and the information will lost forever
model view controller
controller(models.rb) rails routing
1. Routes map incoming url's to controller actions
2. controller actions set instance vairables, visible to views
3. controller action enventually renders a view
Convention over configuration: if naming follows certain conventions, no need for config files
Don't repear yourself: mechanisms to exract common functionality
Database:
Rails feature:
Testing: develpment and production and test enviroments each have own DB
Mirgration: scripts to descripe the change
up version and down version of migration methods, that makes everything reversible
Apply migration to development:
rake db:migrate
Add a new model
rails generate migration
Raisl generate sql statement at runtime, based on ruby code
Subclassing from ActiveRecord::Base
connects a model to a database
Reading things in the database
Movie.where("rating = 'PG')
Add a action
1. create route in config/routes.rb
2. Add the action in the apporcatia place
3. add the view coresspondinly
Debug
Printing to termial
log file
when debugging, the error information can be very useful, the information could tell us where th error is in the ruby.
Don't use puts or printf to print error message, as they may just been print out on the terminal, and the information will lost forever
Wednesday 7 March 2012
Pearson's chi-squared test
source: http://en.wikipedia.org/wiki/Pearson%27s_chi-squared_test
Pearson's chi-squared test (χ2) is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900.[1] In contexts where it is important to make a distinction between the test statistic and its distribution, names similar to Pearson Χ-squared test or statistic are used.
It tests a null hypothesis stating that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable. A simple example is the hypothesis that an ordinary six-sided die is "fair", i.e., all six outcomes are equally likely to occur.
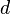 ,
of that statistic, which is essentially the number of frequencies
reduced by the number of parameters of the fitted distribution. In the
third step, X2 is compared to the critical value of no significance from the
,
of that statistic, which is essentially the number of frequencies
reduced by the number of parameters of the fitted distribution. In the
third step, X2 is compared to the critical value of no significance from the  distribution, which in many cases gives a good approximation of the distribution of X2. A test that does not rely on this approximation is Fisher's exact test; it is substantially more accurate in obtaining a significance level, especially with few observations.
distribution, which in many cases gives a good approximation of the distribution of X2. A test that does not rely on this approximation is Fisher's exact test; it is substantially more accurate in obtaining a significance level, especially with few observations.
 observations are divided among
observations are divided among  cells. A simple application is to test the hypothesis that, in the
general population, values would occur in each cell with equal
frequency. The "theoretical frequency" for any cell (under the null
hypothesis of a discrete uniform distribution) is thus calculated as
cells. A simple application is to test the hypothesis that, in the
general population, values would occur in each cell with equal
frequency. The "theoretical frequency" for any cell (under the null
hypothesis of a discrete uniform distribution) is thus calculated as
 , notionally because the observed frequencies
, notionally because the observed frequencies  are constrained to sum to
are constrained to sum to  .
.
 , where
, where  is the number of parameters used in fitting the distribution. For instance, when checking a 3-parameter Weibull distribution,
is the number of parameters used in fitting the distribution. For instance, when checking a 3-parameter Weibull distribution,  , and when checking a normal distribution (where the parameters are mean and standard deviation),
, and when checking a normal distribution (where the parameters are mean and standard deviation),  . In other words, there will be
. In other words, there will be  degrees of freedom, where
degrees of freedom, where  is the number of categories.
is the number of categories.
It should be noted that the degrees of freedom are not based on the number of observations as with a Student's t or F-distribution. For example, if testing for a fair, six-sided die, there would be five degrees of freedom because there are six categories/parameters (each number). The number of times the die is rolled will have absolutely no effect on the number of degrees of freedom.
 The chi-squared statistic can then be used to calculate a p-value by comparing the value of the statistic to a chi-squared distribution. The number of degrees of freedom is equal to the number of cells
The chi-squared statistic can then be used to calculate a p-value by comparing the value of the statistic to a chi-squared distribution. The number of degrees of freedom is equal to the number of cells  , minus the reduction in degrees of freedom,
, minus the reduction in degrees of freedom,  .
.
The result about the number of degrees of freedom is valid when the original data was multinomial and hence the estimated parameters are efficient for minimizing the chi-squared statistic. More generally however, when maximum likelihood estimation does not coincide with minimum chi-squared estimation, the distribution will lie somewhere between a chi-squared distribution with and
and 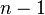 degrees of freedom (See for instance Chernoff and Lehmann, 1954).
degrees of freedom (See for instance Chernoff and Lehmann, 1954).
For the test of independence, also known as the test of homogeneity, a chi-squared probability of less than or equal to 0.05 (or the chi-squared statistic being at or larger than the 0.05 critical point) is commonly interpreted by applied workers as justification for rejecting the null hypothesis that the row variable is independent of the column variable.[2] The alternative hypothesis corresponds to the variables having an association or relationship where the structure of this relationship is not specified.
Pearson's chi-squared test (χ2) is the best-known of several chi-squared tests – statistical procedures whose results are evaluated by reference to the chi-squared distribution. Its properties were first investigated by Karl Pearson in 1900.[1] In contexts where it is important to make a distinction between the test statistic and its distribution, names similar to Pearson Χ-squared test or statistic are used.
It tests a null hypothesis stating that the frequency distribution of certain events observed in a sample is consistent with a particular theoretical distribution. The events considered must be mutually exclusive and have total probability 1. A common case for this is where the events each cover an outcome of a categorical variable. A simple example is the hypothesis that an ordinary six-sided die is "fair", i.e., all six outcomes are equally likely to occur.
Definition
Pearson's chi-squared is used to assess two types of comparison: tests of goodness of fit and tests of independence.- A test of goodness of fit establishes whether or not an observed frequency distribution differs from a theoretical distribution.
- A test of independence assesses whether paired observations on two variables, expressed in a contingency table, are independent of each other—for example, whether people from different regions differ in the frequency with which they report that they support a political candidate.
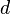 ,
of that statistic, which is essentially the number of frequencies
reduced by the number of parameters of the fitted distribution. In the
third step, X2 is compared to the critical value of no significance from the
,
of that statistic, which is essentially the number of frequencies
reduced by the number of parameters of the fitted distribution. In the
third step, X2 is compared to the critical value of no significance from the  distribution, which in many cases gives a good approximation of the distribution of X2. A test that does not rely on this approximation is Fisher's exact test; it is substantially more accurate in obtaining a significance level, especially with few observations.
distribution, which in many cases gives a good approximation of the distribution of X2. A test that does not rely on this approximation is Fisher's exact test; it is substantially more accurate in obtaining a significance level, especially with few observations.Test for fit of a distribution
Discrete uniform distribution
In this case observations are divided among
observations are divided among  cells. A simple application is to test the hypothesis that, in the
general population, values would occur in each cell with equal
frequency. The "theoretical frequency" for any cell (under the null
hypothesis of a discrete uniform distribution) is thus calculated as
cells. A simple application is to test the hypothesis that, in the
general population, values would occur in each cell with equal
frequency. The "theoretical frequency" for any cell (under the null
hypothesis of a discrete uniform distribution) is thus calculated as , notionally because the observed frequencies
, notionally because the observed frequencies  are constrained to sum to
are constrained to sum to  .
.Other distributions
When testing whether observations are random variables whose distribution belongs to a given family of distributions, the "theoretical frequencies" are calculated using a distribution from that family fitted in some standard way. The reduction in the degrees of freedom is calculated as , where
, where  is the number of parameters used in fitting the distribution. For instance, when checking a 3-parameter Weibull distribution,
is the number of parameters used in fitting the distribution. For instance, when checking a 3-parameter Weibull distribution,  , and when checking a normal distribution (where the parameters are mean and standard deviation),
, and when checking a normal distribution (where the parameters are mean and standard deviation),  . In other words, there will be
. In other words, there will be  degrees of freedom, where
degrees of freedom, where  is the number of categories.
is the number of categories.It should be noted that the degrees of freedom are not based on the number of observations as with a Student's t or F-distribution. For example, if testing for a fair, six-sided die, there would be five degrees of freedom because there are six categories/parameters (each number). The number of times the die is rolled will have absolutely no effect on the number of degrees of freedom.
Calculating the test-statistic
The value of the test-statistic is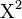 = Pearson's cumulative test statistic, which asymptotically approaches a
= Pearson's cumulative test statistic, which asymptotically approaches a  distribution.
distribution. = an observed frequency;
= an observed frequency; = an expected (theoretical) frequency, asserted by the null hypothesis;
= an expected (theoretical) frequency, asserted by the null hypothesis; = the number of cells in the table.
= the number of cells in the table.

Chi-squared distribution, showing X2 on the x-axis and P-value on the y-axis.
 , minus the reduction in degrees of freedom,
, minus the reduction in degrees of freedom,  .
.The result about the number of degrees of freedom is valid when the original data was multinomial and hence the estimated parameters are efficient for minimizing the chi-squared statistic. More generally however, when maximum likelihood estimation does not coincide with minimum chi-squared estimation, the distribution will lie somewhere between a chi-squared distribution with
 and
and 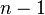 degrees of freedom (See for instance Chernoff and Lehmann, 1954).
degrees of freedom (See for instance Chernoff and Lehmann, 1954).Bayesian method
For more details on this topic, see Categorical distribution#Bayesian statistics.
In Bayesian statistics, one would instead use a Dirichlet distribution as conjugate prior. If one took a uniform prior, then the maximum likelihood estimate for the population probability is the observed probability, and one may compute a credible region around this or another estimate.Test of independence
In this case, an "observation" consists of the values of two outcomes and the null hypothesis is that the occurrence of these outcomes is statistically independent. Each observation is allocated to one cell of a two-dimensional array of cells (called a table) according to the values of the two outcomes. If there are r rows and c columns in the table, the "theoretical frequency" for a cell, given the hypothesis of independence, isFor the test of independence, also known as the test of homogeneity, a chi-squared probability of less than or equal to 0.05 (or the chi-squared statistic being at or larger than the 0.05 critical point) is commonly interpreted by applied workers as justification for rejecting the null hypothesis that the row variable is independent of the column variable.[2] The alternative hypothesis corresponds to the variables having an association or relationship where the structure of this relationship is not specified.
Work Log Mar 6
1. Unix Command
pushd and popd
The
pushd and popd
The
pushd command saves the current working directory in memory so it can be returned to at any time, optionally changing to a new directory. The popd command returns to the path at the top of the directory stack.
Subscribe to:
Posts (Atom)